JavaScript-深入理解浮点数精度问题

本文将从这几个方面带大家去理解JavaScript中的浮点数问题

1、介绍JS的Number

2、0.1 + 0.2 为什么不等于 0.3

3、最大安全数为什么是 2^53 - 1

JS中的Number到底是什么

在深入问题之前，我们先来了解下JS的Number在二进制中是怎么存储的

双精度浮点数

JS中的Number是以双精度浮点数的形式计算的，双精度浮点数总共有8个字节（byte），每字节有8比特（bit-位），即 8bit/byet，所以总共占位64位。

根据IEEE754的标准，双精度浮点数中的占位分为3个部分

这三个部分组成这样一个公式

第一部分：

Sign-符号位，长度是1，0是整数，1是负数

第二部分：

Exponent-指数位（阶码），长度是11，取值范围是[0,2047]（也可以说是0 ~ 2^11-1），本身是无符号位，取值范围是[0,2047]

第三部分

Mantissa-尾数，长度是52

根据第二部分的描述，我们可以把公式优化成这样：

https://pic1.zhimg.com/80/v2-eb41bd8524c33b2920aa41af65fbb02c_1440w.jpg

看完这两个公式，可能有同学开始疑惑了？？？

为什么需要M+1 ？

公式是遵循科学计数法规范的，我们常见的科学计数法是这样的

const a = 2021;
=> 2.21 * 10^3
=> 2.21E3;

二进制中的科学计数法则是这样的

const a = "101011000";
=> 1.01011 * 2^8
// 去除整数部分的1后，剩余 M=01011
// 整数部分只能为1，满足 0 < 整数部分 < 2
// M 是去除1之后剩下的部分，最终计算时需要加回来，所以会有 M+1

为什么需要E-1023 ？

const a = "101011000";
=> 1.01011 * 2^8
// E本身是无符号位，取值范围是[0,2047]，但是指数可以是负数
// 所以IEEE754标准规定，对于E为11位的情况，中间数是 2^10-1=1023
// 正数和负数各占1023个数字

所以E的实际取值范围分为负数[0,1022]，正数[1024,2047]

举个例子

// 举一个我们常用的十进制数字
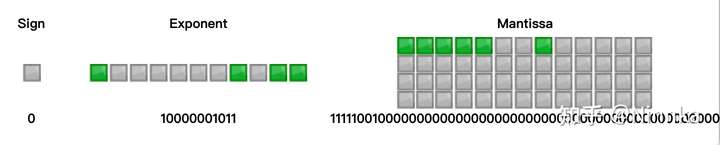
const num = 8080;
// 这个数字转成二进制之后
const numDec = num.toString(2);
=> 1111110010000
// 用科学计数法表示
=> 1.111110010000 * 2^12
E = 12 + 1023 => 10000001011
M = 111110010000{000...000补全到52位}
// 结果如下图

0.1 + 0.2 === 0.3 ？

大家一定经常看到 0.1 + 0.2 这样的送命题，也知道结果肯定不等于0.3

相似的问题还有

0.1 + 0.7 === 0.8 ？
0.2 + 0.4 === 0.6 ？
等等…

问题出现的原因

在我们了解完JS的Number存储机制后，我们分析一下0.1+0.2中出现的问题

先分析0.1

const a = 0.1;
// 转为二进制
const aDec = a.toString(2)
=> 0.000110011001100110011001100110011001100110011001100110011001100{后面循环1100}
// 0.1转为二进制时因为有无限循环，在获取尾数时，第53位需要判断是否为1来进行进位，存在精度丢失
// 因为第53位为1的缘故，最后得到的二进制会比真实的0.1要大
=> 1.1001100110011001100110011001100110011001100110011010 * 2^-4
// 转换回十进制后
=> 1.00000000000000005551115123126E-1
=> 0.100000000000000005551115123126 > 0.1

同理 0.2 也会进行一样的操作

const a = 0.2;
// 转为二进制
const aDec = a.toString(2)
=> 0.001100110011001100110011001100110011001100110011001101{后面循环0011}
// 0.2转为二进制时因为有无限循环，在获取尾数时，第53位需要判断是否为1来进行进位，存在精度丢失
// 因为第53位为1的缘故，最后得到的二进制会比真实的0.2要大
=> 1.100110011001100110011001100110011001100110011001101 * 2^-3
// 转换回十进制后
=> 2.00000000000000011102230246252E-1
=> 0.200000000000000011102230246252 > 0.2

0.1，0.2 两数相加

0.1 + 0.2
=== // 两个对应的二进制相加
0.00011001100110011001100110011001100110011001100110011010
+
0.00110011001100110011001100110011001100110011001100110100

两个二进制数的相加过程

1. 对阶
2. 尾数运算
3. 规格化
4. 舍入
5. 判断溢出

对阶是为了能让让两个数的尾数相加

举个栗子

3.5*10^3 + 8.1*10^2
===
// => 两数的阶码是不同的，前者是3，后者是2，如果他们都是3的话，就可以提取公因式了
3.5*10^3 + 0.81*10^3
=== // 这里可以直接把尾数相加
(3.5 + 0.81)*10^3

回到 0.1 + 0.2 中，首先取两数阶码中较大的那个

0.1 => 0.00011001100110011001100110011001100110011001100110011010 => 2^-4
0.2 => 0.00110011001100110011001100110011001100110011001100110100 => 2^-3
∆E = -3 - (-4) = 1 > 0
// 所以 0.2的阶码大于0.1的阶码
// 先把0.1的尾数向右移 ∆E 位，阶码补∆E
0.00011001100110011001100110011001100110011001100110011010
=> 1.1001100110011001100110011001100110011001100110011010 * 2^-4
// 尾数右移 1 位，左边补1，右移的 1 位遵守0舍1入的原则，这里括号中的 0 是被舍去的
=> 1100110011001100110011001100110011001100110011001101(0)
// 阶码补1
01111111011 => 01111111100
// 最后结果就是
0.1
=> 0;01111111100;1100110011001100110011001100110011001100110011001101

至此，两数阶码相同了，下面开始尾数相加

0.1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1101 * 2^-3
+
1.1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010 * 2^-3
===
=> 10.0110 0110 0110 0110 0110 0110 0110 0110 0110 0110 0110 0110 0111 * 2^-3
===
// 因为整数部分不满足 0 < 整数部分 < 2，所以进行规格化
=> 1.00110 0110 0110 0110 0110 0110 0110 0110 0110 0110 0110 0110 011(1) * 
// 指数位（阶码）进1，尾数右移1位，遵守0舍1入
// 指数由原来的 -3 => -2，E = -2 + 1023 => 01111111101；在E的有效范围内，没有上溢，也没有下溢
=> 1.00110 0110 0110 0110 0110 0110 0110 0110 0110 0110 0110 0110 100 * 2^-2
// 转为非规格二进制形式
=> 0.010011001100110011001100110011001100110011001100110100

二进制转化为十进制就不展开说了

0.010011001100110011001100110011001100110011001100110100
=> 0.30000000000000004440892098500626
// 约定于
≈> 0.30000000000000004

到这里，大家熟悉的结果又出来了

以上就是 0.1 + 0.2 为什么不等于 0.3 的原因

为什么Number在加减乘除后就出现误差，单个就能正常显示

但这里引出了新的疑问，既然0.1和0.2都有精度缺失，那为什么0.1和0.2可以正确表示

const a = 0.1;
a === 0.1 // true

Number.prototype.toPrecision

双精度浮点数的有效尾数是16位，在js中有效位数是17位

可以理解为JS引擎会默认保留最多17位的有效小数

const a = 0.1;
=> (0.1).toPrecision(17)
// 0.100000000000000005551115123126 => 0.10000000000000000(5551115123126)

如何避免计算时的精度误差

第一种，也是常用的方式

在计算过程中把小数都进位到整数后，再进行计算

const a = 0.1;
const b = 0.2;
a + b
=> (a * 10 + b * 10) / 10

第二种

对计算结果做一个精度校准

const a = 0.1;
const b = 0.2;
const c = parseFloat((0.1 + 0.2).toFixed(1))

对精度有很高的要求的场景，比如在算价的场景，建议使用BigInt相关库去操作

推荐一个 bignumberjs

最大安全数为什么是 2^53-1

什么是最大安全数？

最大安全数是指能在JS中不丢失精度的情况下，能表示的最大数字。

通过文档我们可以查到，JS中的最大安全数是2^53-1

MDN MAX_SAFE_INTEGER

Number.MAX_SAFE_INTEGER === 2^53-1 === 9007199254740991

但是为什么说2^53-1是最大的安全数呢？2^53也能正确表示呀

Number.MAX_SAFE_INTEGER + 1 === 2^53 === 9007199254740992

原因在于：从2^53开始，尾数超出了能表示的最大范围，超出的部分被舍去，也就出现了精度上的丢失。

我们可以试着先分析 2^53 - 1

1、分析2^53-1的二进制结构

// 最大安全数的二进制
(2^53-1).toString(2)
// 53位1
=> 11111111111111111111111111111111111111111111111111111
// 规格化后（科学计数法表示）
=> 1.1111111111111111111111111111111111111111111111111111 * 2^52
// 省去整数位，M刚好是52位1，指数位52+1023
=> M = 1111111111111111111111111111111111111111111111111111
=> E = 52 + 1023 = 1075 => 10000110011

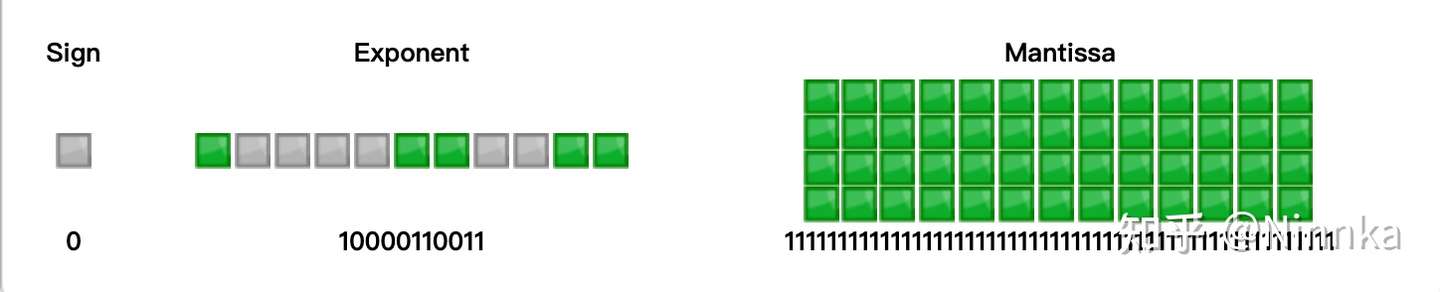
根据IEEE754标准，双精度浮点数中，尾数最多只有52位，当52位都为1时已经是能表示的最大数值了，并且精度未丢失。

我们试着给2^53 - 1加1，也就是Number.MAX_SAFE_INTEGER + 1

Number.MAX_SAFE_INTEGER + 1
// 对阶后，对尾数进行相加
=> 
1.1111111111111111111111111111111111111111111111111111 * 2^52
+ 
0.0000000000000000000000000000000000000000000000000001 * 2^52
=> 10.0000000000000000000000000000000000000000000000000000 * 2^52
// 整数位不满足 0 < N < 2，所以要进行规格化
=> 1.0000000000000000000000000000000000000000000000000000(0) * 2^53
// 整数保留一位后得到新的科学计数法结果，注意尾数有53位0（为了方便看，最后一位用括号包了起来），显然不符合规范
// 由于尾数最多只能用52位表示，我们需要舍去最后一个0
=> 1.0000000000000000000000000000000000000000000000000000 * 2^53
// 结果是：整数位一位1，52位尾数均为0，指数是53

2^53是可以正确表示的，但是从这里开始已经出现了精度丢失，只是因为丢失的是0，所以对结果没有影响，也就不影响展示了

但是丢失的精度会对后续的计算造成很大的影响

我们在用同样的方式算一遍 Number.MAX_SAFE_INTEGER + 2

Number.MAX_SAFE_INTEGER + 2
// 对阶后，对尾数进行相加
=> 
1.1111111111111111111111111111111111111111111111111111 * 2^52
+ 
0.0000000000000000000000000000000000000000000000000010 * 2^52
=> 10.0000000000000000000000000000000000000000000000000001 * 2^52
// 整数位不满足 0 < Integer < 2，所以要进行规格化
=> 1.0000000000000000000000000000000000000000000000000000(1) * 2^53
// 整数保留一位后得到新的科学计数法结果，注意尾数有52位0和1位1（为了方便看，最后一位用括号包了起来），显然不符合规范
// 由于尾数最多只能用52位表示，我们需要舍去最后一个1
=> 1.0000000000000000000000000000000000000000000000000000 * 2^53
// 结果是：整数位一位1，52位尾数均为0，指数是53

注意Number.MAX_SAFE_INTEGER + 2的结果，跟Number.MAX_SAFE_INTEGER + 1是一样的，原因就在于多出的第53位精度丢失了，因为丢的是1，所以影响了最后的结果

Number.MAX_SAFE_INTEGER + 1 === Number.MAX_SAFE_INTEGER + 2

JavaScript 浮点数陷阱及解法
浮点数的二进制表示
JavaScript 浮点数运算的精度问题
二进制浮点数的加减法运算